Write a Leap Year Program in C to check whether the year is Leap Year or Not, using IF-ELSE Statements. The user must enter the Year and Program should Prompt the message "The Entered Year is Leap Year or Not". Leap years have total 366 numbers of days and a February 29. If we need to find which year is Leap Year or not.
- 1992: Leap Year
- 2002: Not a Leap Year
- 2016: Leap Year
- 2100: Not a Leap Year
Leap Year Program in C Using IF-ELSE
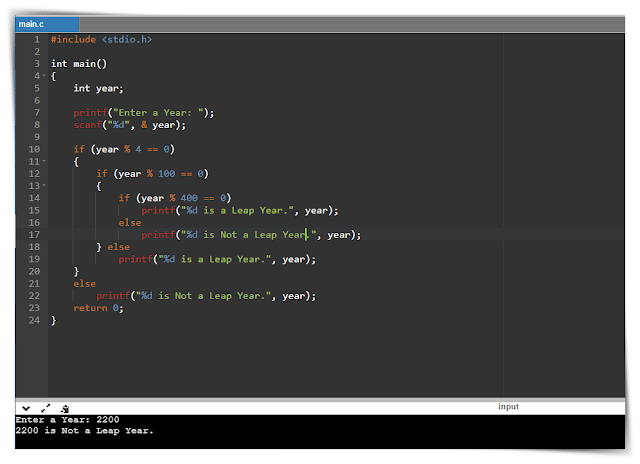
#include <stdio.h>
int main()
{
int year;
printf("Enter a Year: ");
scanf("%d", & year);
if (year % 4 == 0)
{
if (year % 100 == 0)
{
if (year % 400 == 0)
printf("%d is a Leap Year.", year);
else
printf("%d is Not a Leap Year.", year);
} else
printf("%d is a Leap Year.", year);
}
else
printf("%d is Not a Leap Year.", year);
return 0;
}The output of the Leap Year Program in C
Leap Year Program Explanation Step by Step
To Understand this Leap Year Program in C, we have to go with the Line Line Code. So In this, there are the following steps we are going to explain everything in detail.
- Step 1: Take Input from the User, and Store the user value in a variable(As we have stored in a year)
- Step 2: Now the real logic begins, Here the year is divided by then 4 then it's a Leap year, Because as we all know that Leap Year comes every 4 years which is the reason we are going to divide by 4. if (year % 4 == 0), Else print the entered year is not a leap year.
- Step 3: Again We are using Nested IF-ELSE because we have to check for century year(Ex. 1900, 2200, 2300, 2500), Because the Century year is easily divided by 4. So if (year % 100 == 0) this condition is true then we will go to the fourth step. Else print Not a Leap Year.
- Step 4: Now if this if (year % 400 == 0) condition is true then the Year Entered by the user is a Leap Year, and if this condition is not true that means the year is not a Leap Year.
Leap Year Condition
if (year % 4 == 0)
{
if (year % 100 == 0)
{
if (year % 400 == 0)
printf("%d is a Leap Year.", year);
else
printf("%d is Not a Leap Year.", year);
} else
printf("%d is a Leap Year.", year);
}
else
printf("%d is Not a Leap Year.", year);












Why is the post missing a leap year? 2012?
ReplyDelete