Task: The height of a binary search tree is the number of edges between the tree's root and its furthest leaf. You are given a pointer, root, pointing to the root of a binary search tree. Complete the getHeight function provided in your editor so that it returns the height of the binary search tree.
Input Format
Output Format
The locked stub code in your editor will print the integer returned by your getHeight function denoting the height of the BST.
Sample Input
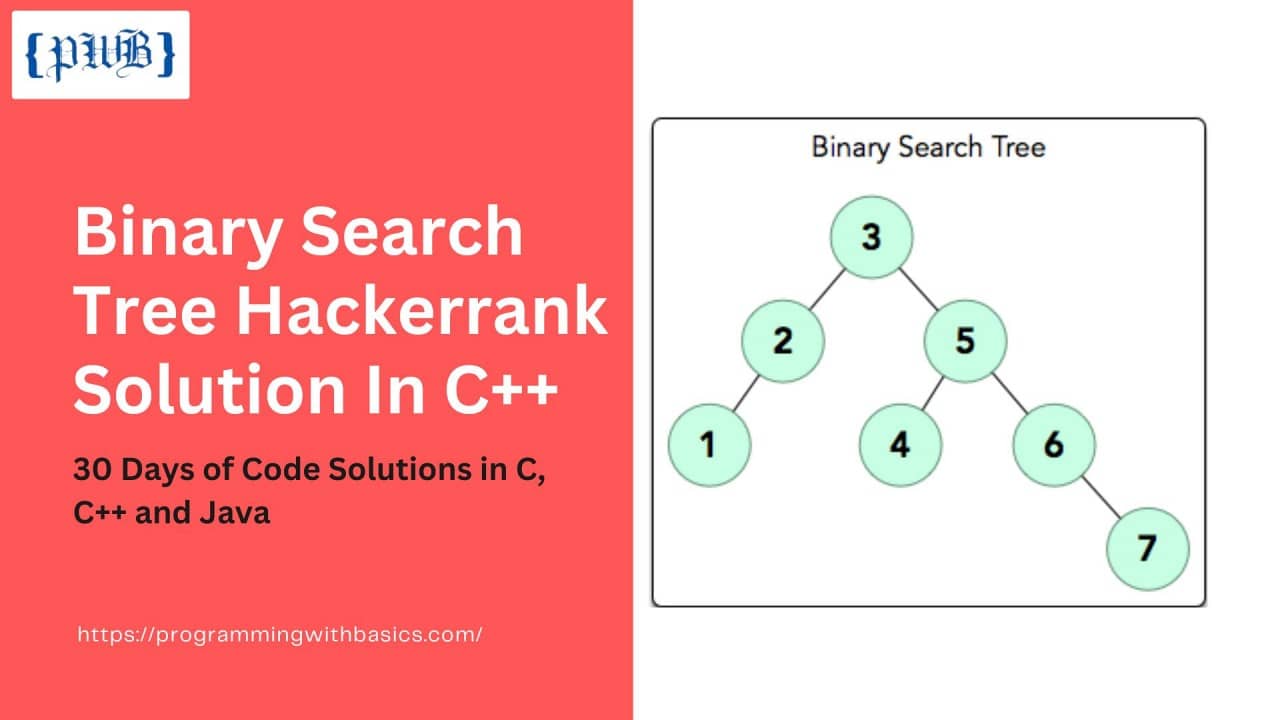
7
3
5
2
1
4
6
7
Sample Output
3
Copy the code and paste it into Hacker rank editor and click to submit button, but before this process, you have to click the below link.
Submit this Solution: Click Here
Input Format
- The locked stub code in your editor reads the following inputs and assembles them into a binary search tree:
- The first line contains an integer, n, denoting the number of nodes in the tree.
- Each of the n subsequent lines contains an integer, data, denoting the value of an element that must be added to the BST.
Output Format
The locked stub code in your editor will print the integer returned by your getHeight function denoting the height of the BST.
Sample Input
7
3
5
2
1
4
6
7
Sample Output
3
Copy the code and paste it into Hacker rank editor and click to submit button, but before this process, you have to click the below link.
Submit this Solution: Click Here
Day 22 Binary Search Tree Hackerrank Solution In C++
#include <iostream>
#include <cstddef>
using namespace std;
class Node {
public: int data;
Node * left;
Node * right;
Node(int d) {
data = d;
left = NULL;
right = NULL;
}
};
class Solution {
public: Node * insert(Node * root, int data) {
if (root == NULL) {
return new Node(data);
} else {
Node * cur;
if (data <= root -> data) {
cur = insert(root -> left, data);
root -> left = cur;
} else {
cur = insert(root -> right, data);
root -> right = cur;
}
return root;
}
}
int getHeight(Node * root) {
//Write your code here
if (!root) {
return -1;
}
int leftDepth = getHeight(root -> left);
int rightDepth = getHeight(root -> right);
return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}
}; //End of Solution
int main() {
Solution myTree;
Node * root = NULL;
int t;
int data;
cin >> t;
while (t--> 0) {
cin >> data;
root = myTree.insert(root, data);
}
int height = myTree.getHeight(root);
cout << height;
return 0;
}Binary Search Tree Time and Space Complexity
| Binary Search Tree Complexity | Average Case | Worst case |
| Space | O(n) | O(n) |
| Search | O(log n) | O(n) |
| Insert | O(log n) | O(n) |
| Delete | O(log n) | O(n) |













0 Comments: